목차
- 시작하면서...
- Product category, Bifunctor
- Product category
- Bifunctor
- Adjoint pair
- Definition
- Remark
- Examples
- free functor
- tensor functor and hom functor
- scalar extension and restriction
- localization
- group ring and G-module
- 마무리
시작하면서...
이번 포스팅에서는 대수 공부할 때 알게모르게 쓰였던 adjoint pair에 관하여 다뤄보고자 한다.
Product category, Bifunctor
Product category
두 category $\mathcal{C}$, $\mathcal{C}'$이 주어졌다고 하자.
$\mathcal{C}$와 $\mathcal{C}'$의 product $\mathcal{C}\times\mathcal{C}'$는 다음과 같이 정의된다.:
object: $$ Ob(\mathcal{C}\times\mathcal{C}'):= Ob(\mathcal{C})\times Ob(\mathcal{C}') $$
morphism: 주어진 object pairs $(A,A'),(B,B')\in\mathcal{C}\times\mathcal{C}'$에 대하여, $$ Hom_{\mathcal{C}\times\mathcal{C}'}((A,A'),(B,B')):=Hom_{\mathcal{C}}(A,B)\times Hom_{\mathcal{C}'}(A',B') $$
composition은 componentwise하게 정의된다. 즉, 적당히 합성 잘 되게끔 morphisms $(f,g),(h,k)$를 뽑으면, 다음과 같이 정의된다.:
$$ (h,k)\circ (f,g):=(h\circ f, k\circ g) $$
그러면 실제로 $$\mathcal{C}\times\mathcal{C}'$$은 category가 됨은 쉽게 확인할 수 있다.
Bifunctor
Categories $\mathcal{C},\mathcal{C}',\mathcal{D}$에 대하여 functor $$H:\mathcal{C}\times\mathcal{C}'\longrightarrow\mathcal{D}$$를 bifunctor라 한다. 즉, product category에서 다른 category로 가는 functor를 bifunctor라 하는 것인데, 실제로 bifunctor가 됨을 보일 때에는 한 component를 고정하고 다른 하나에 대하여 각각 functor가 됨을 보이기만 하면 충분하다. 이유는 아래의 식이 성립하기 때문이다.:
$$ (f,g)=(f,id)\circ (id,g) $$
Adjoint pair
Definition
두 functor $F:\mathcal{C}\longrightarrow\mathcal{C}'$와 $G:\mathcal{C}'\longrightarrow\mathcal{C}$가 주어졌다고 하자. 이 때 $F,G$가 adjoint pair다, 혹은 $F$가 $G$에 left adjoint되어있다 (혹은 $G$가 $F$에 right adjoint되어있다) 라는 것은 아래의 bifunctor 사이의 natural isomorphism이 성립할 때이다.:
$$ Hom_{\mathcal{C}'}(F(\bullet),\bullet)\cong Hom_{\mathcal{C}}(\bullet,G(\bullet)) $$
다시 말해, 임의의 object $A\in\mathcal{C}$, $B\in\mathcal{C}'$에 대하여, 아래의 natural bijection이 성립한다는 뜻이다.
$$ Hom_{\mathcal{C}'}(FA,B)\cong Hom_{\mathcal{C}}(A,GB) $$
기호로는 $F\dashv G$로 표기한다.
Remark
바로 위의 식에서 특별한 경우로써, $A\in\mathcal{C}$가 주어질 때마다 $FA\in\mathcal{C}'$이므로 다음의 식을 얻을 수 있다.
$$ Hom_{\mathcal{C}'}(FA,FA)\cong Hom_{\mathcal{C}}(A,GFA) $$
이 때 왼쪽의 hom set에는 $id_{FA}$가 있는걸 안다. 위의 bijection으로부터 $id$에 대응하는 morphism $\eta_A:A\longrightarrow GFA$를 canonical morphism이라고 한다.
이 때 각 $A\in\mathcal{C}$마다 canonical morphism $\eta_A$가 정의되는데, 실제로 이는 $A$에 관해 natural하므로 $$\eta:id_{\mathcal{C}}\longrightarrow GF,\quad\eta=(\eta_A)_{A\in\mathcal{C}}$$는 natural transformation이 된다.
$\eta$의 naturality는 adjunction의 naturality로부터 나온다. 실제로 임의의 $\mathcal{C}$의 morphism $f:A\longrightarrow B$가 주어졌을 때 $Ff:FA\longrightarrow FB$에 대해 아래 두 adjunction의 naturality
$$ Hom_{\mathcal{C}'}(FA,\bullet)\cong Hom_{\mathcal{C}}(A, G(\bullet)) $$
$$ Hom_{\mathcal{C}'}(F(\bullet), B)\cong Hom_{\mathcal{C}}(\bullet, GB) $$
를 이용하면 아래와 같은 commutative diagram을 얻는다.

이로부터 $$ \eta_B\circ f = GFf\circ\eta_A $$가 성립함을 알고, 이것은 정확히 $\eta$의 naturality를 설명하는 식이다. diagram으로 보면 아래와 같다.

비슷하게 각 $B\in\mathcal{C}'$이 주어질 때마다 특별한 bijection $$ Hom_{\mathcal{C}}(GB,GB)\cong Hom_{\mathcal{C}'}(FGB,B) $$를 얻고, 이 때 $id_{GB}$에 대응하는 canonical morphism $\xi_B:FGB\longrightarrow B$를 얻는다. 이 또한 adjunction의 naturality로부터 natural transformation $$\xi:FG\longrightarrow id_{\mathcal{C}'},\quad\xi=(\xi_B)_{B\in\mathcal{C}'}$$를 얻었다.
Examples
Free Functor
처음으로 살펴볼 것은 free functor가 forgetful functor에 left adjoint되어 있다는 것이다.
좀 더 구체적으로, $$A\in\mathtt{CRINGS}$$를 하나 고정하고 아래의 두 functor를 정의한다.
$$ F:\mathtt{SETS}\longrightarrow A\text{-}\mathtt{MOD},\quad S\mapsto FS $$
where $FS$ is a free $A$-module generateed by $S$, and
$$ U:A\text{-}\mathtt{MOD}\longrightarrow\mathtt{SETS},\quad M\mapsto UM $$
where $UM$ is equal to $M$ as a set.
그러면 $F\dashv U$가 된다.
이를 보이기 위해서는 다음의 natural bijection이 성립함을 보이면 충분하다.:
$$ Hom_{A\text{-}\mathtt{MOD}}(FS,M)\cong Hom_{\mathtt{SETS}}(S,UM) $$ which is natural in $S$ and $M$.
canonical map $\iota:S\mapsto FS$에 대하여, $A$-linear map $\varphi:FS\longrightarrow M$마다 map $\varphi\circ\iota:S\longrightarrow M$으로 대응시키고, map $f:S\longrightarrow M$가 주어질 때마다 free module의 universal property로부터 unique $A$-linear map $\overline{f}:FS\longrightarrow M$ such that $\overline{f}\circ\iota=f$를 얻고 이를 대응시킨다. 그러면 이 두 함수는 서로 inverse 관계가 됨을 밝히며 bijection임을 보일 수 있다.
naturality는 아래 두 commutative diagram으로 대체한다.
(이 때 $f:S_1\longrightarrow S_2$는 set map, $\psi:M_1\longrightarrow M_2$는 $A$-linear map.)


그러므로 $F\dashv U$임을 안다.
이 사실로부터 set map $S\longrightarrow M$이 있을 때마다 $A$-linear map $FS\longrightarrow M$을 항상 구할 수 있고, $A$-linear map $FS\longrightarrow M$은 the set of generators $S$의 함숫값에 의해서 유일하게 결정됨을 안다. $FS$에서 $M$으로 가는 $A$-linear map이라고 하면 $FS$의 생김새 때문에, 혹은 더 생각하지 않고 당연히 $S$에서의 함숫값만 생각했을 수도 있지만, 사실은 정말로 그것만 생각하면 충분하다는 뜻을 함의하고 있는 것이다.
tensor functor and hom functor
다음으로 commutative algebra, 51:06에서 보였던 natural bijection $$ Hom_{A\text{-}\mathtt{MOD}}(M\otimes_A N, P)\cong Hom_{A\text{-}\mathtt{MOD}}(M, Hom_{A\text{-}\mathtt{MOD}}(N,P)) $$ which is natural in $M$ and $P$를 보이고자 한다. (지금 보니 세미나에서는 bijection임만 보이고 naturality는 보이지 않았다.) 이는 adjunction의 언어로 표현하자면 $A$-module $N$에 대하여 $-\otimes_A N\dashv Hom_{A\text{-}\mathtt{MOD}}(N,-)$이다.
처음부터 다시 해보자. 이번에는 pushforward, pullback의 언어를 써서 표현해보고자 한다.
canonical $A$-bilinear map $\otimes:M\times N\longrightarrow M\otimes_A N$에 대하여, $A$-linear map $\varphi:M\otimes_A N\longrightarrow P$가 주어질 때마다 $A$-bilinear map $\varphi\circ\otimes:M\times N\longrightarrow P$를 얻을 수 있다. 이는 $\otimes$의 pullback을 $\otimes^*$라고 쓰면 $\otimes^*(\varphi)=\varphi\circ\otimes$이 된다. 이로부터 $A$-linear map $\psi:M\longrightarrow Hom_{A\text{-}\mathtt{MOD}}(N,P)$ defined by $\psi(m):=\otimes^*(\varphi)_m$ where $\otimes^*(\varphi)_m(n):=\otimes^*(\varphi)(m,n)$을 구할 수 있어서 mapping $\varphi\mapsto\psi$을 하나 얻었다.
역으로 $A$-linear map $\xi:M\longrightarrow Hom_{A\text{-}\mathtt{MOD}}(N,P)$가 주어질 때마다 $A$-bilinear map $\eta:M\times N\longrightarrow P$ defined by $\eta(m,n):=\xi(m)(n)$을 얻을 수 있고, tensor product의 universal property에 의해 unique $A$-linear map $\overline{\eta}:M\otimes_A N\longrightarrow P$ such that $\overline{\eta}\circ\otimes=\eta$를 구할 수 있다. 이로부터 mapping $\xi\mapsto\overline{\eta}$를 하나 더 얻었다.
이 두 맵이 서로 inverse 관계가 있음을 보이면 우선 bijection이 되는 것까지는 보일 수 있게 된다.
다음으로 naturality를 확인해야 한다. 이것도 commutative diagram만 쓰고 넘기려고 했으나 적어도 나에게는 그 과정이 클리어하지 않았었기 때문에 자세한 풀이를 기록으로 남겨둔다. 우선 $A$-linear map $\alpha:M_1\longrightarrow M_2$에 대하여 다음의 diagram이 commute하는지, 즉 아래 점선이 실제로 성립하는지 보면 된다.

이는 아래와 같이 실제로 계산해보면 같음을 확인할 수 있다.
$$ \begin{aligned} \alpha^*(\psi)(m_1)(n) &= \bigg((\psi\circ\alpha)(m_1)\bigg)(n) \\ &= \bigg(\psi(\alpha(m_1))\bigg)(n) \\ &= (\otimes^*(\varphi))_{\alpha(m_1)}(n) \\ &= (\otimes^*(\varphi))(\alpha(m_1),n) \\ &= (\varphi\circ\otimes)(\alpha(m_1),n) \\ &= \varphi(\alpha(m_1)\otimes n) \end{aligned} $$
$$ \begin{aligned} \xi(m_1)(n) &= \bigg(\otimes^*\bigg((\alpha\otimes N)^*(\varphi)\bigg)\bigg)_{m_1}(n) \\ &= \bigg(\otimes^*\bigg((\alpha\otimes N)^*(\varphi)\bigg)\bigg)(m_1,n) \\ &= \bigg((\alpha\otimes N)^*(\varphi)\bigg)(m_1\otimes n) \\ &= \varphi\circ(\alpha\otimes N)(m_1\otimes n) \\ &= \varphi(\alpha(m_1)\otimes n) \end{aligned} $$
이로부터 $M$에 대한 naturality는 보였다.
위와 비슷하게 $P$에 대한 naturality를 보이기 위해서는 $A$$linear map $\beta:P_1\longrightarrow P_2$에 대하여 아래의 diagram이 commute하는지 보면 된다.
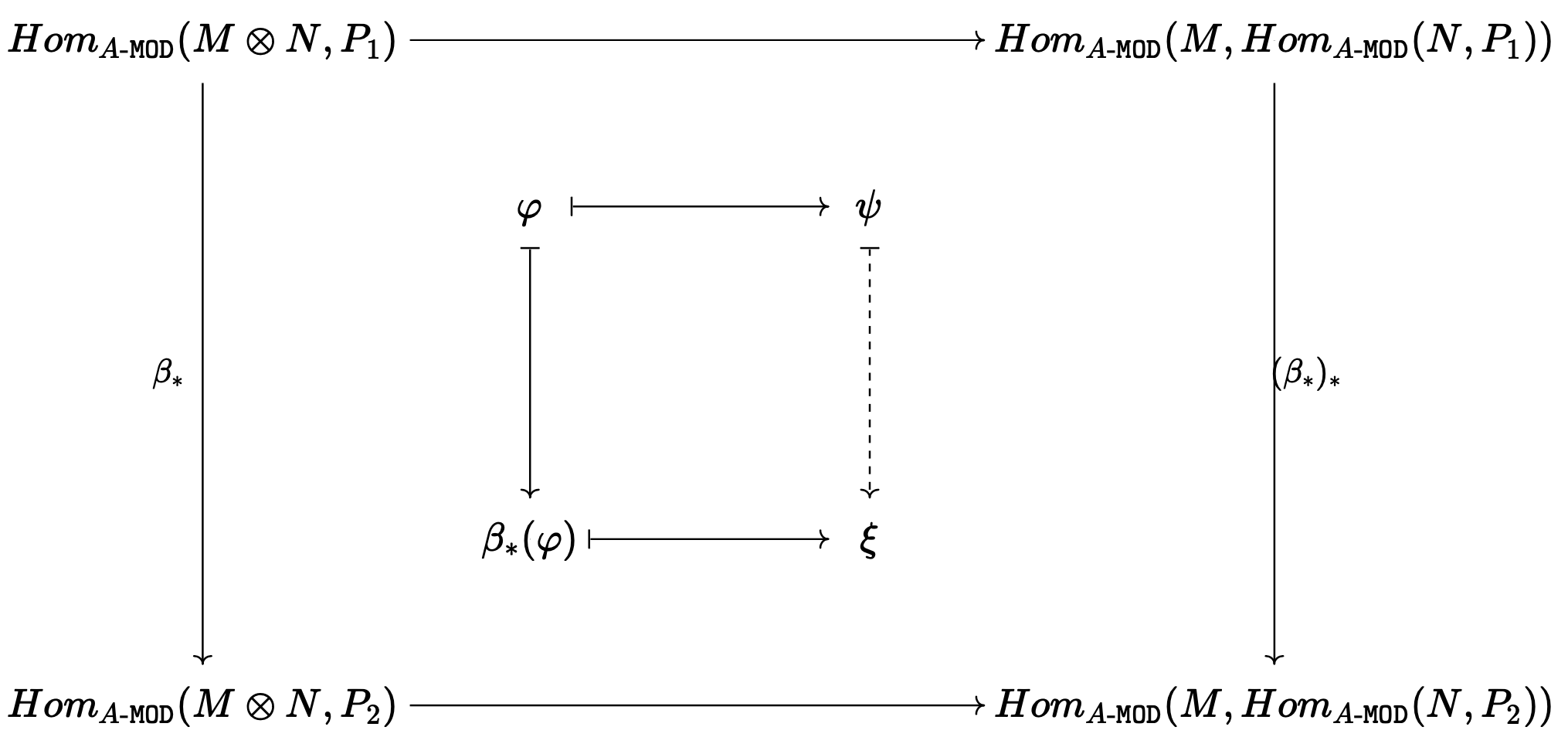
이것 또한 차근차근 전개해보면 실제로 같은 것을 확인할 수 있다. (이 때 $\beta_*$은 $\beta$의 pushforward이다.)
$$ \begin{aligned} \bigg((\beta_*)_*\psi\bigg)(m)(n) &= \bigg(\beta_*\circ\psi\bigg)(m)(n) \\ &= \beta_*(\psi(m))(n) \\ &= (\beta\circ\psi(m))(n) \\ &= \beta\bigg(\bigg(\psi(m)\bigg)(n)\bigg) \\ &= \beta\bigg((\varphi\circ\otimes)_m(n)\bigg) \\ &= \beta\bigg((\varphi\circ\otimes)(m,n)\bigg) \\ &= \beta(\varphi(m\otimes n)) \end{aligned} $$
$$ \begin{aligned} \xi(m)(n) &= \bigg(\otimes^*\bigg(\beta_*(\varphi)\bigg)\bigg)_m(n) \\ &= \bigg(\otimes^*\bigg(\beta_*(\varphi)\bigg)\bigg)(m,n) \\ &= \bigg(\beta_*(\varphi)\bigg)(m\otimes n) \\ &= (\beta\circ\varphi)(m\otimes n) \\ &= \beta(\varphi(m\otimes n)) \end{aligned} $$
그러므로 $P$에 대해서도 naturality를 확인하면서 증명을 마친다.
Scalar Extension and Restriction
이번에는 scalar extension 및 restriction을 adjunction의 관점에서 접근해보고자 한다.
ring homomorphism $f:A\longrightarrow B$, $A$-module $M$, $B$-module $N$이 주어졌다고 하자. 그러면 $-\otimes_A B\dashv (N\mapsto N_A)$이다. 여기서 $N_A$는 $B$-module $N$을 주어진 ring homomorphism $f$를 이용하여 $A$-module로 만든 것이다. 즉, scalar multiplication을 다음과 같이 준다.
$$ a\cdot n:=f(a)n $$
위의 adjunction을 보인다는 것은 다음의 natural bijection을 보이는 것과 같다.
$$ Hom_{B\text{-}\mathtt{MOD}}(M\otimes_A B,N)\cong Hom_{A\text{-}\mathtt{MOD}}(M,N_A) $$
which is natural in $M$ and $N$.
canonical map $\xi:M\longrightarrow M\otimes_A B,\quad\xi(m)=m\otimes 1$에 대하여, $B$-linear map $\varphi:M\otimes_A B\longrightarrow N$이 주어질 때마다 $A$-linear map $\xi^*(\varphi)=\varphi\circ\xi$를 얻을 수 있다. 이로부터 한쪽 mapping $\varphi\mapsto\xi^*(\varphi)$을 안다. 역으로 $A$-linear map $\psi:M\longrightarrow N_A$가 주어질 때마다 $B$-bilinear map $\eta:M\times B\longrightarrow N,\quad\eta(m,b):=b\psi(m)$을 구할 수 있고 tensor product의 universal property로부터 unique $B$-linear map $\overline{\eta}:M\otimes_A B\longrightarrow N$ such that $\overline{\eta}\circ\otimes=\eta$를 얻는다. 이로부터 반대쪽 mapping $\psi\mapsto\overline{\eta}$를 구할 수 있고, 이 두 mapping은 서로 inverse 관계에 있어서 우리가 원하는 bijection이 보여지게 된다.
adjuction이 가지는 naturality에 대한 증명은 생략한다.
Localization
commutative algebra에서 빼놓을 수 없는 것이 바로 localization이다. 우리는 localization으로부터 자연스러운 extension을 알고 있는데 복습하자면 다음과 같다. commutative ring $A$와 multiplicative subset $S$$of $A$가 주어져 있을 때, $A$-module $M$에 대하여 $S^{-1}M$은 $S^{-1}A$-module이 되고 $S^{-1}A$-module로써 다음의 isomorphism이 성립한다.
$$ M\otimes_A S^{-1}A\cong S^{-1}M $$
localization이 갖는 canonical ring homomophism $A\longrightarrow S^{-1}A$에 대하여 바로 앞에서 했던 논의를 적용하면 $S^{-1}A$-module $N$도 $A$-module로써 이해할 수 있게 된다. 이로부터 다음의 natural bijection을 얻는다. (즉, 이는 위의 논의의 special case이다.)
$$ Hom_{S^{-1}A\text{-}\mathtt{MOD}}(S^{-1}M,N)\cong Hom_{A\text{-}\mathtt{MOD}}(M,N) $$
which is natural in $M$ and $N$.
Group Ring and G-module
group $G$가 주어져 있을 때 $\mathbb{Z}$-algebra $\mathbb{Z}[G]$를 정의하고자 한다. 우선 underlying abelian group은
$$ \oplus_{g\in G}\:\mathbb{Z}g $$
이다. 이 때 $\mathbb{Z}g:=\{ng\::\:n\in\mathbb{Z}\}$이고 direct sum으로 정의했기 때문에 원소는
$$ \sum_{g\in G} n_g g $$
where $n_g=0$ for all but finitely many $g\in G$ 로 정의된다. multiplication은 아래와 같은 convolution product로 정의된다.
$$ \bigg(\sum_g n_g g\bigg)\cdot\bigg(\sum_g m_g g\bigg):=\sum_g\bigg(\sum_{hk=g} n_h m_k\bigg)g. $$
scalar multiplication은
$$ m\cdot\bigg(\sum_g n_g g\bigg):=\sum_g (mn_g) g $$
로 정의한다. 그러면 실제로 $\mathbb{Z}[G]$는 $\mathbb{Z}$-algebra structure를 갖게 되고 이를 group ring이라 부른다. 사실은 $\mathbb{Z}$뿐만 아니라 일반적인 ring에 대해서도 방금과 같이 group ring의 정의를 할 수 있고, 특별히 이 ring이 commutative한 경우에는 group algebra라고 부른다.
group homomorphism $\varphi:G\longrightarrow H$가 주어질 때마다 induced ring homomorphism $$\mathbb{Z}[G]\longrightarrow\mathbb{Z}[H],\quad g\mapsto\varphi(g)$$ for all $g\in G$를 얻을 수 있다.
다시 본론으로 돌아오면, 결국 $\mathbb{Z}[-]$는 $\mathtt{GRP}\longrightarrow\mathtt{RINGS}$인 functor로 볼 수 있다. 반대로 $\mathtt{RINGS}\longrightarrow\mathtt{GRP}$인 functor 중에서는 ring $R$이 주어질 때마다 unit group $R^{\times}$로 대응시키는 functor를 생각할 수 있다. 이제 전달하고자 하는 사실은 $\mathbb{Z}[-]$는 unit group으로 대응시키는 functor에 left adjoint되어 있다는 사실이다. 즉, 다음의 natural bijection이 성립한다.
$$ Hom_{\mathtt{RINGS}}(\mathbb{Z}[G],R)\cong Hom_{\mathtt{GRP}}(G,R^{\times}) $$
which is natural in $G$ and $R$.
특별히 $R$에 대해서도 natural하니 abelian group $A$에 대하여 endomorphism ring $R=End_{\mathbb{Z}}(A)$을 택해보면 다음의 bijection도 얻게 된다.
$$ Hom_{\mathtt{RINGS}}(\mathbb{Z}[G],End_{\mathbb{Z}}(A))\cong Hom_{\mathtt{GRP}}(G,Aut_{\mathbb{Z}}(A)) $$
이 natural bijection이 말해주는 바는 무엇인가? 일반적으로 abelian group $A$위에 module structure를 준다는 것은 ring homomorphism $R\longrightarrow End_{\mathbb{Z}}(A)$를 하나 주는 것과 같다. 그런 의미에서 보면 위 bijection에서 왼쪽은 abelian group위에 $\mathbb{Z}[G]$-module structure를 주는 방법을 의미한다. 이에 대응하여 오른쪽을 보면 group homomorphism $G\longrightarrow Aut_{\mathbb{Z}}(A)$를 하나 얻게 되는데, 이는 마치 abelian group 위에서 group $G$가 acting 하는 것처럼 보인다. 이러한 structure를 $G$-module structure 혹은 group representation이라고 하고 이 때의 $A$를 G-module이라고 부른다.
마무리
adjunction의 naturality를 보이다보니 이제는 naturality를 증명하는 것에서는 어느정도 자유를 얻은 것 같다. 그리고 adjunction이 이렇게 여기저기에 스며 들어가 있었다는 점이 놀라웠다.
'Math > Category Theory' 카테고리의 다른 글
| [Category] 9. Limit and Colimit (0) | 2022.07.21 |
|---|---|
| [Category] 8. Product and Coproduct (0) | 2022.07.21 |
| [Category] 6. Representable Functor (0) | 2022.07.21 |
| [Category] 5. Yoneda Lemma (0) | 2022.07.21 |
| [Category] 4. Equivalence of Categories (0) | 2022.07.20 |