목차
- 시작하면서...
- Category of presheaves 정의
- Yoneda embedding 정의
- Yoneda lemma
- Yoneda lemma 의미
- Yoneda lemma 증명
- Corollary 1
- Corollary 2
- 마무리
시작하면서...
이번 포스팅에서는 yoneda lemma와 이에 관련한 corollary 몇가지를 살펴보고자 한다.
yoneda lemma 및 yoneda embedding이 어떤 의미가 있는지에 대해 나의 생각을 적어놓고자 한다.
Category of presheaves 정의
$\mathcal{C}$를 category라고 하자. 이 때 $$\mathcal{C}^{\wedge}:=Fct(\mathcal{C}^{op},\mathtt{SETS})$$ 를 the category of presheaves라 한다.
즉, $\mathcal{C}^{\wedge}$는 contravariant functor $\mathcal{C}\longrightarrow\mathtt{SETS}$의 category인 것이다. 이 때의 contravariant functor를 presheaf라고 한다.
Yoneda embedding 정의
$X\in\mathcal{C}$마다 contravariant functor $h_X:\mathcal{C}\longrightarrow\mathtt{SETS}$를 다음과 같이 정의하고자 한다.:
$$h_X(Y):=Hom_{\mathcal{C}}(Y,X)$$ for each $Y\in\mathcal{C}.$
그러면 $h_X\in C^{\wedge}$이다.
이로부터 functor $h:\mathcal{C}\longrightarrow\mathcal{C}^{\wedge}$는 다음과 같이 정의된다.:
$$X\mapsto h_X,$$ $$(f:Y\longrightarrow Y')\mapsto (f^*:Hom_{\mathcal{C}}(Y',X)\longrightarrow Hom_{\mathcal{C}}(Y,X),\: g\mapsto g\circ f).$$
이 때의 $h$를 yoneda embedding이라 부른다.
Yoneda lemma
우선 Yoneda lemma의 statement는 다음과 같다.
각 $F\in\mathcal{C}^{\wedge}$와 $X\in\mathcal{C}$에 대해, 다음의 bijection이 존재한다.: $$Hom_{\mathcal{C}^{\wedge}}(h_X,F)\cong F(X)$$
이 때 위 관계식은 $X$와 $F$에 관해 natural 하다.
Yoneda lemma 의미
위 식이 주는 의미는 무엇인가? 이를 이해하기 위해서 필요한 정의들을 하나하나 되짚어 나가보았다.
우선 일반적으로 두 category가 있다고 해보자. 그러면 이 둘의 구조적 관계성을 보여주는 것이 functor일 것이다.
이러한 두 category 사이의 functor는 일반적으로 무수히 많을 것이다. 그래서 이 functor 사이의 관계성을 파악하기 위해 morphism of functors에 해당하는 natural transformation을 정의했었다.
즉, 우리는 natural transformation을 통해 두 category 사이의 functor들 간의 관계를 얘기해볼 수 있을 것이다.
한편, 우리는 set theory에 익숙하고 따라서 미지의 대상을 이해할 때 set으로 치환하여 이해할 수 있으면 좋을 것 같다.
그래서 이해하고 싶은 category가 하나 있으면, 이 category에서 $\mathtt{SETS}$로 가는 functor를 생각해볼 수 있다. 여기서 yoneda lemma와 결을 맞추기 위해 contravariant functor를 잡았다고 해보자.
막상 functor를 잡기는 했는데, 너무나 막막하다. 아까 위에서 말했듯, 두 category 사이에는 어마어마하게 많은 functor들이 있고 이러한 문제는 $\mathtt{SETS}$로 보낸다고 해서 해결될 건 아닐 것이다.
하지만 우리에게는 그나마 익숙한 contravariant functor $Hom_{\mathcal{C}}(\bullet, X)$가 있다. 따라서 이를 기준으로 생각하면 좋겠다. 즉, $\mathcal{C}$에서 $\mathtt{SETS}$로 가는 임의의 contravariant functor와 방금 잡은 hom functor 사이의 natural transformation을 다 모아놓아 보자.
여기서 Yoneda lemma가 말해주는 바가 있는 것이다. Yoneda lemma에 의하면, 이러한 contravariant functor 사이의 morphisms는, 사실 우리가 알고자 하는 임의의 contravariant functor를 통한 object의 image와 같다는 것이다.
심지어 이 관계성을 얻기 위해서 설정해왔던 고정된 object $X$와 contravariant functor $F:\mathcal{C}\longrightarrow\mathtt{SETS}$에 대해서 natural하기 때문에, 즉, $X$와 $F$에 의존하는 relation이 아니기 때문에 더 가치가 있다.
$X$와 $F$를 빼고 생각했을 때 보이는 구조적 동질성이 실제로 Yoneda lemma에서 말하고자 하는 것일거라 생각한다.
Yoneda lemma 증명
우선 bijection임을 보이기 위해 다음의 두 set map을 정의한다.
$$\xi:Hom_{\mathcal{C}^{\wedge}}(h_X,A)\longrightarrow A(X),\quad\alpha\mapsto\alpha_X(id_X)$$
$$\eta:A(X)\longrightarrow Hom_{\mathcal{C}^{\wedge}}(h_X,A),\quad x\mapsto\tilde{x}$$ where $\tilde{x}$ is a natural transformation consisting of $\tilde{x}_Y:Hom_{\mathcal{C}}(Y,X)\longrightarrow A(Y)$ given by $\tilde{x}_Y(f):=A(f)(x)$ for each $Y\in\mathcal{C}$ and $f\in Hom_{\mathcal{C}}(Y,X).$
이 두 map이 서로 inverse라는 것을 보이면 원하는 bijection을 보일 수 있다.
우선 $\eta\circ\xi=id_{Hom_{\mathcal{C}^{\wedge}}(h_X,A)}$가 됨을 보여보자.
이는 임의의 natural transformation $\alpha:h_X\longrightarrow A$와 $\mathcal{C}$의 morphism $f:Y\longrightarrow X$$에 대하여,
$$A(f)\bigg(\alpha_X(id_X)\bigg)=\alpha_Y(f)$$
를 확인하는 것과 같다. ($\eta$의 $x$자리에 $\xi(\alpha)$를 넣고...)
그런데 이는 이미 성립하고 있다. 왜냐하면 $\alpha$가 naturality를 갖고 있기 때문이다. 아래 commutative diagram을 보라.

따라서 $\eta\circ\xi=id_{Hom_{\mathcal{C}^{\wedge}}(h_X,A)}$가 성립함을 안다.
이제 반대로 $\xi\circ\eta=id_{A(X)}$임을 보여보자.
이는 임의의 $x\in A(X)$에 대해 $\eta(x)_X(id_X)=x$인지만 파악하면 되는데, 아래와 같이 손쉽게 파악이 가능하다.
$$\eta(x)_X(id_X)=A(id_X)(x)=id_{A(X)}(x)=x.$$
이로부터 $\xi\circ\eta=id_{A(X)}$ 또한 성립하고, 그러므로 원하는 bijection을 보이게 됐다.
이제 이 bijection이 $X$와 $A$에 대해서도 natural함을 보여보도록 하자.
우선 $X$에 대한 naturality, 즉 아래의 식을 확인해본다.
$$ Hom_{\mathcal{C}^{\wedge}}(h_{\bullet},A)\cong A(\bullet) $$
좌변을 $F$로 쓰면 $F:\mathcal{C}\longrightarrow\mathtt{SETS}$는 다음을 만족시키는 contravariant functor이다.:
object는 $X\in\mathcal{C}$마다 $$F(X)=Hom_{\mathcal{C}^{\wedge}}(h_X, A)$$로 대응시키고,
morphism은 $g:X\longrightarrow X'$ in $\mathcal{C}$마다 $$Fg:Hom_{\mathcal{C}^{\wedge}}(h_{X'},A)\longrightarrow Hom_{\mathcal{C}^{\wedge}}(h_X,A),\quad (\alpha_Y)\mapsto (\beta_Y)$$ where 각 $Y\in\mathcal{C}$마다 $\beta_Y:Hom_{\mathcal{C}}(Y,X)\longrightarrow A(Y)$는 $\beta_Y(f):=\alpha_Y(g\circ f)$ for each $f:Y\longrightarrow X$이다.
이제 $F\cong A$ naturally를 보이기 위해 $\epsilon:F\longrightarrow A$를 다음과 같이 정의하자.:
각 $X\in\mathcal{C}$마다 $\epsilon_X:FX\longrightarrow AX$는 위에서 정의한 bijection이다.
각 $g:X\longrightarrow X'$마다 다음의 commutative diagram을 만족시키는 것을 보이면 $\epsilon$이 natural isomorphism임을 안다.
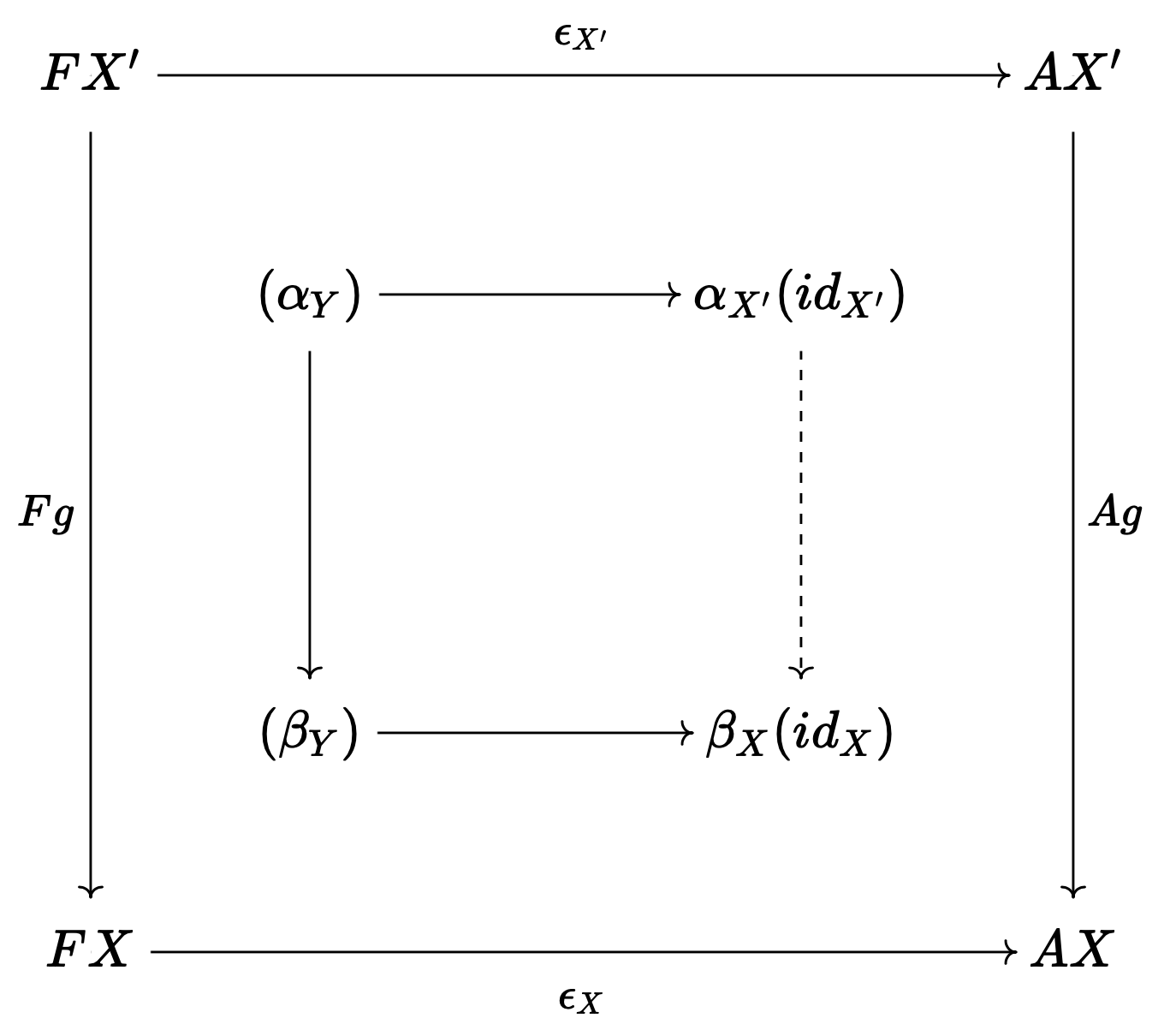
결국 이는 $Ag\bigg(\alpha_{X'}(id_{X'})\bigg)=\beta_X(id_X)(=\alpha_X(g\circ id_X)=\alpha_X(g))$가 성립하는지를 보는 것과 같다.
실제로 이 식이 성립하는 것을 알 수 있는데, 그 이유는 $\alpha$가 natural transformation이기 때문이다. 즉, 위의 $g:X\longrightarrow X'$에 대하여 $\alpha$의 naturality를 서술하면 아래의 diagram과 같다.

그러므로 $\epsilon$은 natural isomorphism이 된다.
다음으로 $A$에 대한 naturality, 즉 다음을 확인한다.
$$ Hom_{\mathcal{C}^{\wedge}}(h_X,\bullet)\cong\bullet(X) $$
좌변의 functor $G:\mathcal{C}^{\wedge}\longrightarrow\mathtt{SETS}$는 다음과 같이 정의된 covariant functor이다.:
object는 각 $A\in\mathcal{C}^{\wedge}$마다 $$G(A):=Hom_{\mathcal{C}^{\wedge}}(h_X,A)$$로 대응되고,
morphism은 $\gamma:A\longrightarrow A'$마다 $$G\gamma:Hom_{\mathcal{C}^{\wedge}}(h_X,A)\longrightarrow Hom_{\mathcal{C}^{\wedge}}(h_X,A'),\quad\alpha\mapsto\gamma\circ\alpha$$로 정의된다.
우변의 functor $H:\mathcal{C}^{\wedge}\longrightarrow\mathtt{SETS}$는 각 $A\in\mathcal{C}^{\wedge}$마다 $H(A):=AX$로 대응되고, 각 $\gamma:A\longrightarrow A'$마다 $H\gamma:=\gamma_X$로 정의된다.
이제 $G\cong H$ naturally를 보이기 위해 $\delta:G\longrightarrow H$를 다음과 같이 정의하자.:
각 $A\in\mathcal{C}^{\wedge}$마다 $\delta_A:GA\longrightarrow HA$는 위에서 보인 bijection이다.
$\delta$가 natural isomorphism임을 보이려면, 각 $\gamma:A\longrightarrow A'$ in $\mathcal{C}^{\wedge}$마다 아래의 diagram이 commute하는지 보면 된다. 그런데, 이는 $\gamma$가 갖는 naturality로부터 바로 보여진다.
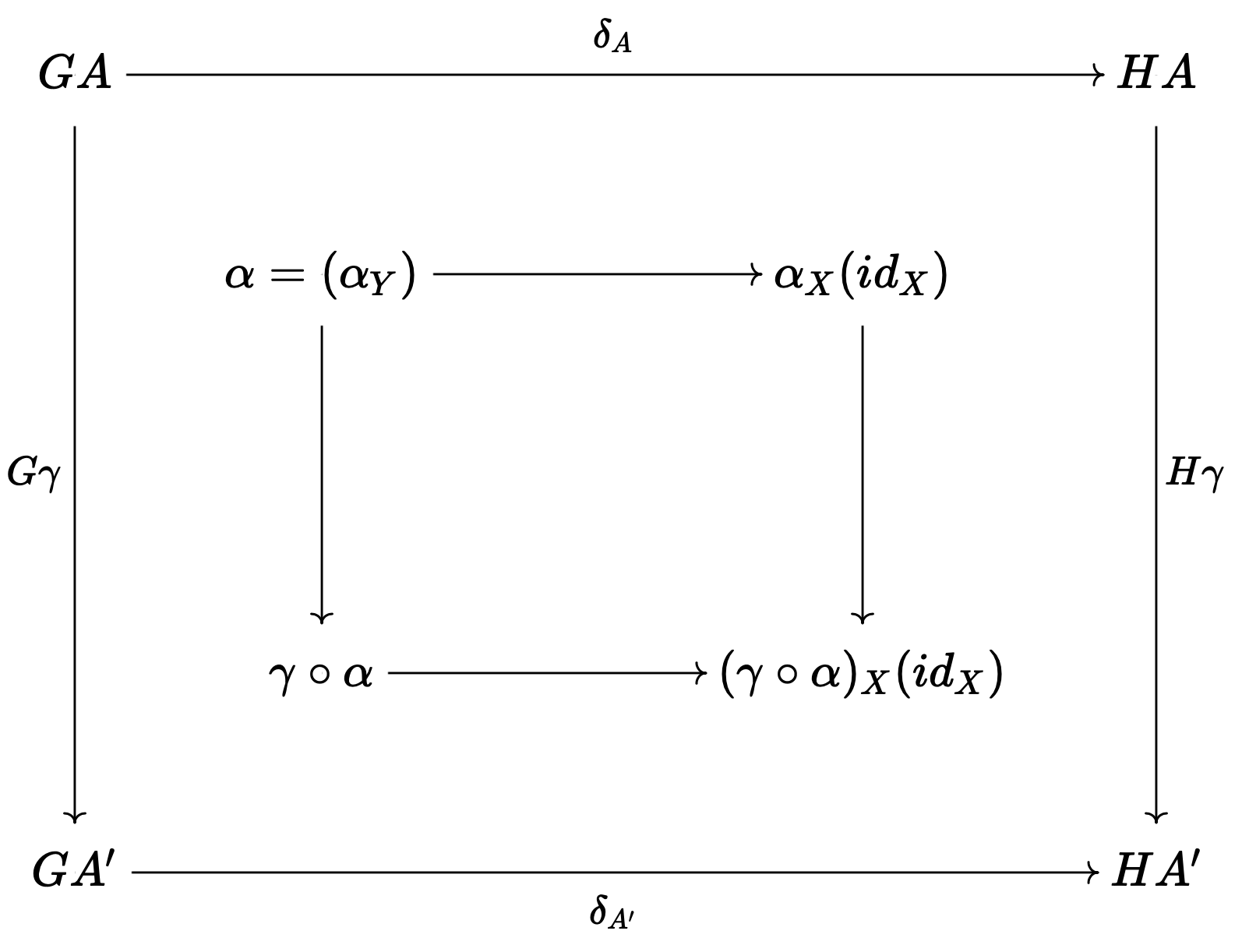
그러므로 $\delta$ 또한 natural isomorphism이다.
이로부터 Yoneda lemma의 증명을 마친다.
Corollary 1
The functor $h:\mathcal{C}\longrightarrow\mathcal{C}^{\wedge}$ is fully faithful.
이는 Yoneda lemma에서 $A:=h_Y$로 택하면 바로 보여진다.
$$ Hom_{\mathcal{C}^{\wedge}}(h_X, h_Y)\cong Hom_{\mathcal{C}}(X,Y) $$
Corollary 2
Let $\mathcal{C}$ be a category. Let $f:X\longrightarrow Y$ be a morphism in $\mathcal{C}$. If $h_f$ is an isomorphism in $\mathcal{C}^{\wedge}$, then $f$ is an isomorphism in $\mathcal{C}$.
이 결과는 Corollary 1로부터 바로 도출된다.
마무리
이번 포스팅은 Yoneda lemma에 대해서 알아보았다. Hom functor는 역시 괜히 배운게 아니었다. 다음 포스팅에서는 Hom functor에 대해서 좀 더 알아보는, representable functor에 대해서 알아보도록 하겠다.
'Math > Category Theory' 카테고리의 다른 글
| [Category] 7. Adjoint Pair (0) | 2022.07.21 |
|---|---|
| [Category] 6. Representable Functor (0) | 2022.07.21 |
| [Category] 4. Equivalence of Categories (0) | 2022.07.20 |
| [Category] 3. Natural Transformation (0) | 2022.07.20 |
| [Category] 2. Functor (0) | 2022.07.20 |