목차
- 시작하면서...
- Natural transformation 정의
- Examples
- 마무리
시작하면서...
드디어 natural transformation에 대해 다룰 시간이 왔다. 정의가 다소 복잡하여 처음에는 이해하기 어려웠으나, 사실 지금도 이해했다고 하면 과장된 것 같지만, 어쨌든 내 나름의 방식대로 이해를 해보았다. 지나고 보면 알고 난 후에는 별게 아닐지라도, 이러한 과정들이 굉장히 값진 과정이라는걸 알기에 기록으로 남겨둔다.
보통 natural transformation을 확인하는 것은 막상 쓰기에는 꽤 귀찮은 작업이어서 책의 저자들은 대부분 이를 생략한다. 본 포스팅에서는 좀 귀찮긴 하지만 기록용이니까 풀이를 가능한 한 감추지 않으려고 한다.
Natural transformation 정의
Category는 object와 morphism으로 이루어져 있다. Category는 정의상 각 object마다 identity morphism을 가지므로, 사실상 morphism만으로 이루어져 있다고 봐도 큰 무리는 아닌 것 같다. 이러한 측면에서 functor란 결국 두 카테고리의 구조적 동질성(composition을 해서 보내나 보내고 composition을 하나 같음)을 얘기하는 것이다. 그렇다면 functor 사이의 morphism, 즉 natural transformation은 어떤 정의를 이루어야 할까? 하나의 morphism을 두 개의 functor가 보냈을 때, 이 둘을 서로 잘 어울리도록 하는 무언가면 좋겠다. 이러한 관점에서 정의를 보면 그리 억지스럽지 않다.
$F,G:\mathcal{C}\longrightarrow\mathcal{D}$가 functors라고 하자. 이 때 $F$와 $G$ 사이의 morphism(or natural transformation) $\alpha:F\longrightarrow G$는 아래의 조건을 만족시키는 $\mathcal{D}$의 morphism collection $\{\alpha_X\::\:FX\longrightarrow GX\}_{X\in\mathcal{C}}$이다.:
임의의 morphism $$f:X\longrightarrow Y$$에 대하여 아래의 diagram이 commutative하다.
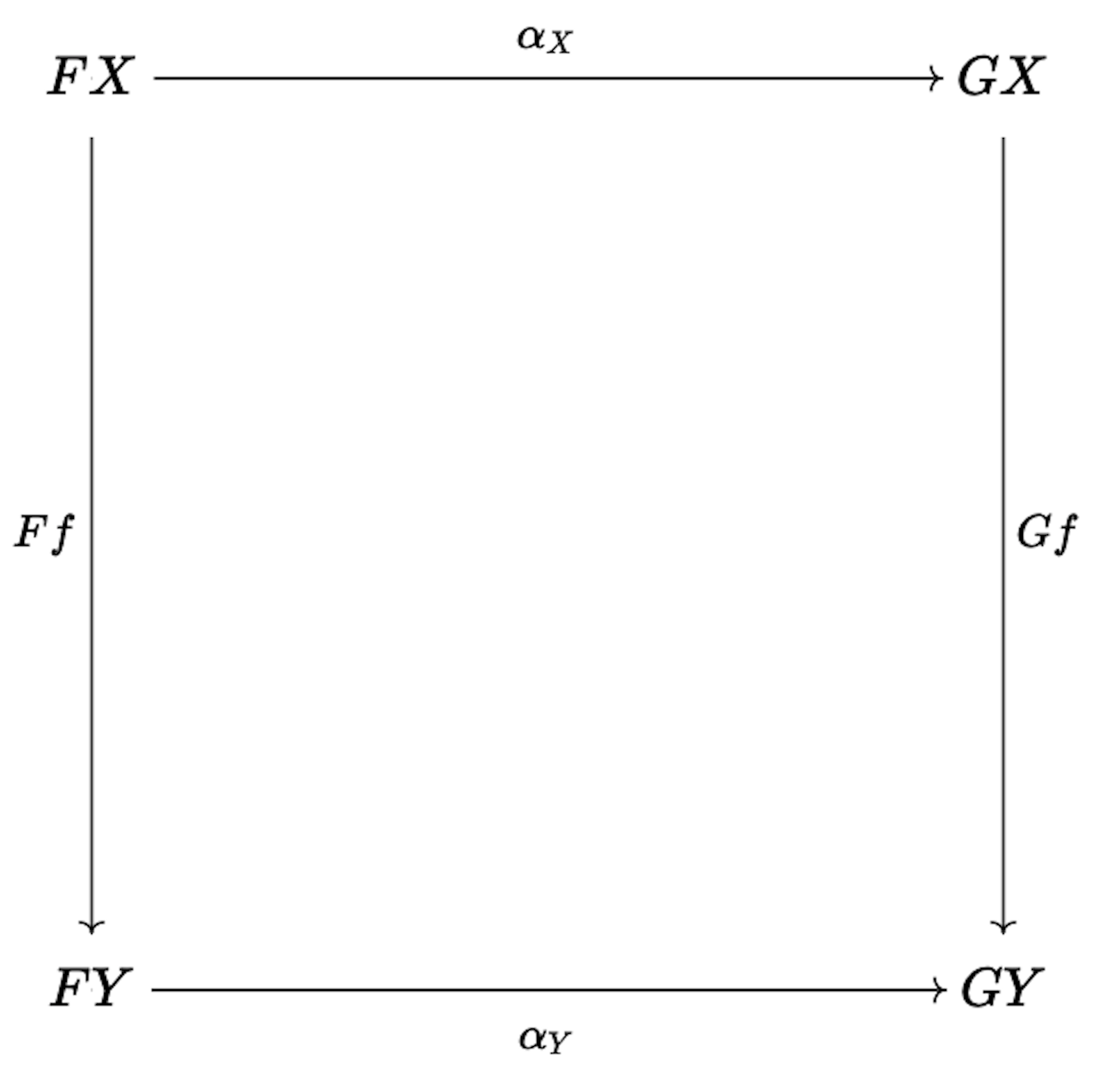
만약 각 $X\in\mathcal{C}$에 대하여 $\alpha_X$가 isomorphism이라면, 이 때의 $\alpha$를 isomorphism(or natural isomorphism)이라고 부른다.
Examples
1. $k$를 field라 하고 category $k\text{-}\mathtt{VECT}$를 고려하자. $k$-vecctor space가 주어질 때마다 이에 대응하는 dual space와 double dual space가 있다는 것은 선형대수를 통해서 이미 알고 있는 사실이다. 이는 $k\text{-}\mathtt{VECT}$ 사이에서 정의된 functor로 이해할 수 있다. 이를 각각 $(-)^{\vee}$와 $(-)^{\vee\vee}$로 표기하자. 이제 선형대수에서 공부했었던
Vector space와 double dual space는 naturally isomorphic하다.
라는 명제를 실제로 보이고자 한다. 이는 finite dimensional vector space 일 때 성립하므로 이 예에서는 $k\text{-}\mathtt{VECT}$를 finite dimensional vector space의 category라고 가정(위 명제가 성립하는 vector space를 reflexive하다고 한다. finite dimension이면 reflexive인 것이다.)하고 아래의 morphism이 natural isomorphism이 되는 것을 보이고자 한다.: $$ c: id_{k\text{-}\mathtt{VECT}}\longrightarrow(-)^{\vee\vee}. $$
이 morphism은 다음과 같은 morphism들로 구성이 되어있다.: $$c_V:V\longrightarrow V^{\vee\vee}$$ for each $$V\in k\text{-}\mathtt{VECT}.$$
각 $V\in k\text{-}\mathtt{VECT},\:v\in V$마다 $c_V(v):V^{\vee}\longrightarrow k$는 $c_V(v):=ev_v$ (evaluation map)으로 정의되며, $ev_v(f):=f(v)$로 정의된다.
우선 $c$가 실제로 natural transformation이 되는지 먼저 확인해보자. 이는 결국 다음의 diagram이 commutative인지 확인하면 되는 문제이다.:
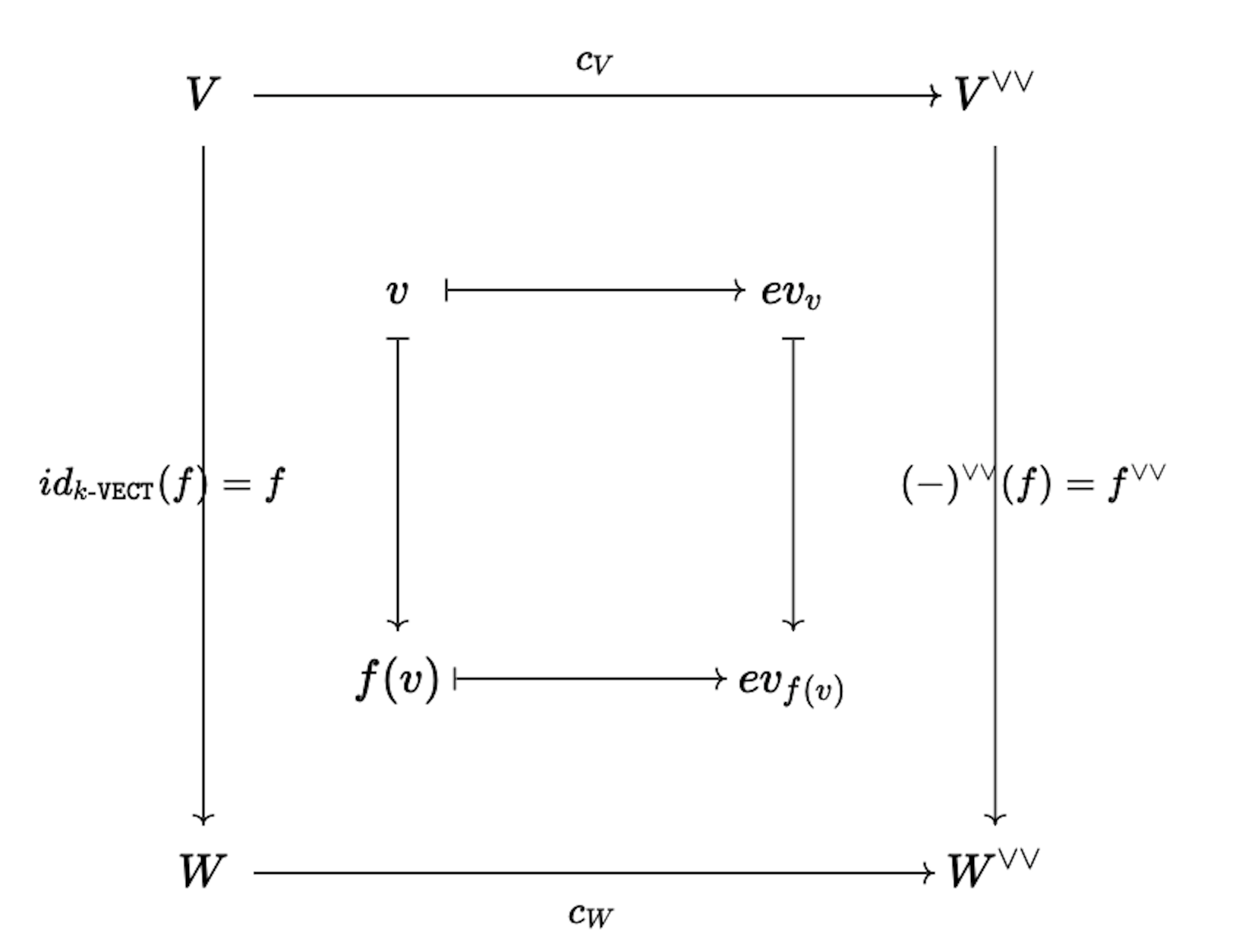
실제로 임의의 $k$-linear map $g:W\longrightarrow k$에 대하여 $ev_{f(v)}(g)=g(f(v))$이고, $$ \begin{aligned} f^{\vee\vee}(ev_v)(g) &= (ev_v\circ f^{\vee})(g) \\ &= ev_v(f^{\vee}(g)) \\ &= ev_v(g\circ f) \\ &= (g\circ f)(v) \\ &= g(f(v)) \end{aligned} $$ 이므로 위 diagram은 commutative하다. 따라서 $c$는 natural transformation이다. 증명에서 알 수 있듯 natural transformation 까지는 dimension 제한 없이 일반적인 vector space에서 성립한다.
여기서 vector space를 finite dimensional vector space만으로 제한하면, its double dual vector space 또한 같은 dimension을 갖기 때문에, 각 $c_V$가 isomorphism인 것을 알 수 있다. 그러므로 $c$는 natural isomorphism이다.
2. 다음으로 commutative ring의 category를 $\mathtt{CRINGS}$이라고 하자. 고정된 자연수 $n$에 대하여, 다음과 같은 functor를 정의하자.: $$ M_n:\mathtt{CRINGS}\longrightarrow\mathtt{RINGS},\:A\mapsto M_n(A). $$
여기서 $M_n(A)$는 $A$의 원소를 entry로 갖는 $n\times n$ square matrix의 모임이다. 그러면 forgetful functor $U:\mathtt{CRINGS}\longrightarrow\mathtt{RINGS}$에 대하여 $\det:M_n\longrightarrow U$는 natural transformation이 된다.
$\det$는 선형대수에서 했듯 주어진 commutative ring $A$에 대해 matrix $K=(k_{ij})\in M_n(A)$가 주어지면 $$ \det_A(K):=\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{i=1}^n k_{\sigma(i)i} $$로 정의되는 함수다. 이제 다음의 diagram이 commutative인지 확인해보도록 하겠다.:

임의의 commutative ring homomorphism $f:A\longrightarrow B$에 대하여, $U(f)$는 commutativity를 잃어버린 ring homomorphism $A\longrightarrow B$이다. 아래 식의 $f$는 $U(f)$를 의미한다. $$ \begin{aligned} f(\det_A((k_{ij}))) &= f(\sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{i=1}^n k_{\sigma(i)i}) \\ &= \sum_{\sigma\in S_n}\text{sgn}(\sigma)\prod_{i=1}^n f(k_{\sigma(i)i}) \\ &= \det_B((f(k_{ij}))) \end{aligned} $$ 이므로 commutative 함을 확인하였다. 위 풀이에서 $f$가 적용될 때 commutative가 적용되지 않아도 된다는 점이 주목해야 할 포인트이다.
결국 이 natural transformation이 말해주는 바는 무엇인가? $M_n$과 $U$라는 functor들은 commutative ring을 ring으로 바꿔주는 적당한 방법을 각각 제시한다. $M_n$은 commutative ring이 주어질 때마다 이를 entry를 갖는 matrix로, $U$는 그저 commutativity만 잃어버리도록 한다. 생김새는 완전히 다르게 주었지만, 결국 이 둘 사이는 $\det$라는 morphism에 의해 연결되어 있음을 확인했다. 즉, 이 예를 통하여 우리는 natural transformation이 구체적인 생김새에 의존하지 않고 구조적 동질성에만 집중할 수 있도록 도와준다는 것을 알 수 있고, 이 예의 경우 $\det$가 그런 역할을 하는 함수라는 것을 안 것이다.
마무리
이번 포스팅에서는 natural transformation과 natural isomorphism이 무엇인지 알아보았다. 계산도 직접 해봐야 하는건 두말하면 잔소리고, 함의하는 의미를 파악하려고 노력하는 것이 상당히 중요한 부분 같다. 다음 포스팅에서는 두 개의 category가 equivalent하다는 것이 무엇인지 다뤄보도록 하겠다.
'Math > Category Theory' 카테고리의 다른 글
| [Category] 6. Representable Functor (0) | 2022.07.21 |
|---|---|
| [Category] 5. Yoneda Lemma (0) | 2022.07.21 |
| [Category] 4. Equivalence of Categories (0) | 2022.07.20 |
| [Category] 2. Functor (0) | 2022.07.20 |
| [Category] 1. Category, Isomorphism (4) | 2022.07.19 |